This post assumes that the reader understands the SSA style of compiler IR, and is familiar with lattice based data flow analyses.

Using Speculation to Help Optimization

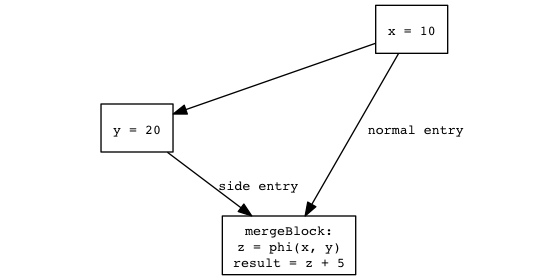
Normal SSA based data flow analyses compute facts based on a conservative but sound worst case – it assumes that every path in the control flow graph that may be taken is taken. However, profiling data (collecting this data correctly is a non-trivial problem, but we won’t talk about that here) may show us that, in practice, some viable branches are almost never taken. Consider the following flow graph:

(Figure A)

Since the optimizer has to assume that both normal entry and side entry are viable paths into mergeBlock, the only information it has about z is that it is either 10 or 20. The computation of result can’t thus be constant folded. To be clear, normal entry and side entry are just names in this context – they don’t mean anything specific.

If, via profiling, we notice that the side entry edge is almost never taken, we can conclude that the value of z is 10 and constant fold result. Operationally we do this by installing a “trap” on the uncommon path:

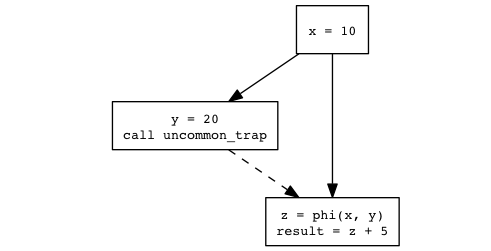
(Figure B)

which effectively exits the function (more explanation forthcoming). The dashed line then becomes a non-viable path (never taken), and z is now the constant 10. In other words, we speculatively optimize with the added assumption “the branch side entry will never be taken”. Hopefully this assumption will hold for a vast majority of the times the compiled code is invoked.

Now, even when the assumption we made speculatively turns out to be incorrect (i.e. the program does end up taking the “never taken” branch), the speculatively optimized version of the function needs to do something meaningful and sane. There are many ways to skin this cat: a runtime with a JIT compiler may decide to implement uncommon_trap as a side exit to the interpreter, while a static compiler may decide to bail out to another, “safer” pre-compiled version of the same method. There is a cost associated with installing these “deoptimization points” though – for static compilers, the number of copies of subsections of the method is exponential in the number of assumptions, leading to code bloat; for a JITed environment there is the runtime cost of going from running the compiled version of a method to running it in the interpreter when the uncommon_trap is actually taken, which may be quite severe. This gets us out of the preamble and to the real topic I wanted to write about …

A Lattice for Speculative DFA: Motivation

Consider this (contrived) case:

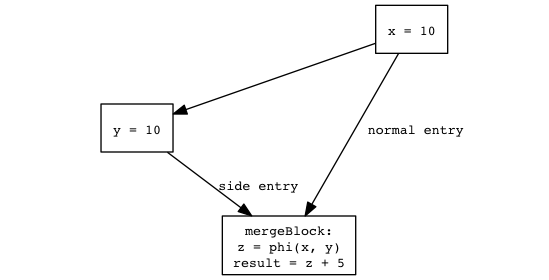
(Figure C)

Installing an uncommon_trap before side entry now no longer helps constant propagation (since side entry or no side entry, z is a constant 10), and whether we want an uncommon_trap before side entry or not is a matter of asking if the reduced code size helps performance – an arguably less interesting question. Even if side entry is taken in one out of ten million executions, the benefit of having a slightly smaller code footprint may be overshadowed by the cost of exiting back to the interpreter (because of the uncommon_trap) for just that one execution. (I’ve tacitly switched to talking about speculative optimizations in a JITed runtime, as that is the scenario I’m most familiar with.)

A more direct and limited way of framing the question is, given a CFG and a DFA analysis framed in terms of a lattice and transfer functions, which branches, when elided, help optimization? When is it profitable to insert an uncommon_trap call? Perhaps too naively, a branch can be profitably elided if the performance of the interpreter when the branch is taken and the performance of the optimized program when the branch is not taken, weighed by the branch probabilities is better overall. In other words, if we had a meaningful way of computing the impact of a branch elision on optimization, we could estimate if eliding the branch more than compensates for the times we will have to take the slow uncommon_trap and jump back to the interpreter.

An assumption worth restating more clearly is that we already have a set of edges that profiling tells us is “rarely taken”, and wish to know if eliding any of those edges improves optimization – checking all (or a non-trivially large subset of) the \(2^{edges}\) possibilities will be prohibitively expensive. Normally JIT compilers end up installing traps in most of these edges, hoping that the cost of the occasional side exit to the interpreter is worth the added performance in the fast case. We want a way to push the decision on whether to install a trap for a specific edge to later in the optimization process.

A Lattice for Speculative DFA: Construction

A regular DFA produces a solution that maps SSA variables to lattice elements conservatively estimating some property of the variable. The first observation is that instead of mapping SSA variables to “static” lattice values that represent a conservative answer, we can map them to functions which map sets of viable edges (the edges that may possibly be traversed) to lattice values. For instance, in Figure A, z can be mapped to a function that takes a set of edges E to return NotConstant if both normal entry and side entry are in E, but return Constant if only of them is in E.

The second observation is that we can take an existing lattice based DFA, and transform it to a DFA of the above kind, whose solution maps SSA variables to functions, in a fairly straightforward way.

• transfer functions remain essentially the same – instead of adding fact \(F\), you add the fact \(\lambda S \to F\). What we’re basically saying is that transfer functions produce facts that are not sensitive to edge elision. e.g. in Figure A, we’d add \(\lambda S \to y = Constant(20)\) to our fact set as we encounter y = 20.

• meet handles the edge-set sensitive aspect of the scheme. Given a meet \(\wedge\) over the regular, edge-insensitive lattice; we construct our meet \(\wedge_{f}(In = \{V_0, V_1 \cdots V_n\})\) \(=\) \(\lambda S\) \(\to\) \(\bigwedge\limits_{v \, \in \, In \: \&\& \: E(v) \, \in \, S} v(S)\) where \(E(v)\) is the edge corresponding to the incoming value \(v\). Intuitively, the function that a phi node maps to returns the meet of the incoming lattice values whose incoming edge is in the edge set that was passed in.

Once we have these lattice values (which are functions, really) for each SSA variable, we are now able to answer the question “which expressions constant fold if we elide edge \(e\)?”.

So far we’ve only considered constant propagation, but only because it is simple to analyze. I think this technique should be generalizable to any lattice based DFA.

Conclusion

I haven’t spent any time thinking about the soundness of this construction. The first next step is be to prove that the new DFA actually does reach a fixed point; and to somehow solve the problem of comparing functions as values (how do we know the lattice element for a specific SSA variable has changed?).

Frankly, I don’t think this construction is suitable for implementation in its current form. Taking this to production (if it can be proven to be sound) will probably involve taking some sort of a hybrid approach.